これまでのプログラムで球面や球体をよく扱ってきました。これらの球(正確には三角ポリゴンで構成された多面体)はなめらかさを調整できるよういつもコードで生成しているのですが、極に近づくにつれ密度が高まる形をしています。これはざっくりいうと平面の等間隔グリッドをくるりと丸めるような作り方をしているため。この方法だと計算が簡単なのです。正距円筒図法のテクスチャも貼りやすい。
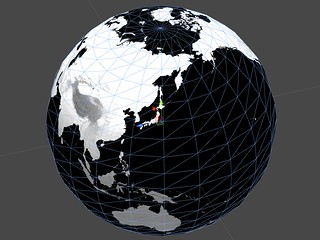
Unity標準のSphereオブジェクトも同様の形状。赤道付近にくらべ北極付近のポリゴンが細かいことがわかる(水色の線)
通常はこれで十分なのですが、ポリゴンに疎密があると扱いにくいケースがたまにあります。そこでいわゆる「ジオデシックドーム」を生成してみることにしました。
ジオデシックドームとは、正三角形、ないしそれに近い三角形で構成された球状の多面体のこと。正三角形は三辺の長さが等しく、それが敷き詰められているのだから、頂点同士の距離は均等になります。密度はしたがって一定です。
概念はわかったものの、均等な頂点座標をいったいどう求めればいいのか? 数学は苦手なので、適当にググってみます。すると、次のような手順がわかりました。
- 正二十面体を作る
- 正二十面体を構成する正三角形を複数の正三角形に分割する
- 分割した正三角形の頂点を、正二十面体に外接する球の表面へ移動させる
正二十面体は正三角形20枚で構成された凸正多面体です。その正三角形のそれぞれを、たとえばトライフォースのように4つの正三角形に分割します。分割することで増えた(この場合3つの)頂点を、球の中央から外側の方向へ、もとの正二十面体が外接する球の表面まで移動させます。こうして増えた新たな三角形は、同じ要領でさらに分割できます。これを再帰的に繰り返すことでなめらかな球面に近づけることができるのです。
肝心の、基となる正二十面体の頂点座標は決め打ちで持つことにしました。『正20面体の頂点座標の求め方』によると(方法が意外でおもしろい)、次の12点です。
- (±1, ±G, 0) ※Gは黄金比 (1+√5)/2
- (0, ±1, ±G)
- (±G, 0, ±1)
以上、わかってしまえばロジックは簡単。素直に実装するとジオデシックドームができました。
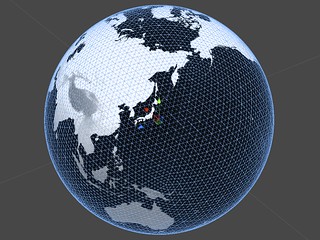
0回(正二十面体のまま)から3回までの再帰分割結果。ポリゴンに疎密は見られない
5回分割、計27,300ポリゴン。2~4分割くらいが実用的か。なおこうした球や筒など表面の両端がつながっているメッシュでは境界のUV座標に要注意。端に向かって1.0に近づくが、境界をまたいだ途端0.0に戻るため、適切に処理しないとそこだけおかしな見た目になる。あと、Mesh.RecalculateNormalsの罠にも注意…